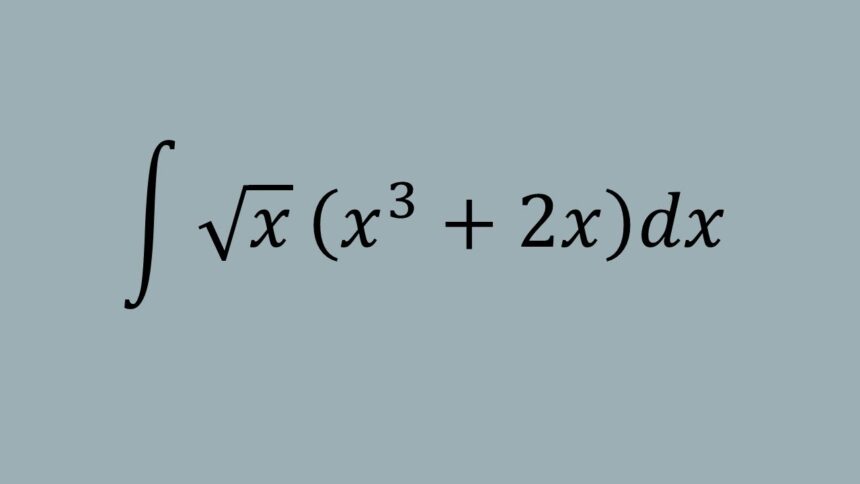Have you ever encountered a mathematical concept that seemed to bridge the gap between abstract theory and practical application? Intégrammes represent exactly that kind of fascinating intersection in mathematics, combining the elegance of integral calculus with innovative problem-solving approaches.
This comprehensive guide will take you through everything you need to know about intégrammes, from their fundamental principles to advanced applications. Whether you’re a student struggling with calculus concepts or a professional seeking to expand your mathematical toolkit, understanding intégrammes can significantly enhance your analytical capabilities.
By the end of this post, you’ll have a solid grasp of what makes intégrammes unique, how to approach them systematically, and why they’re becoming increasingly important in various fields of study and application.
Understanding Intégrammes and Their Mathematical Significance
Intégrammes represent a specialized approach to integration problems that combines visual representation with analytical techniques. Unlike traditional integration methods that rely solely on algebraic manipulation, intégrammes incorporate graphical elements that help visualize the integration process.
The significance of intégrammes extends beyond mere computational convenience. They serve as powerful tools for understanding the geometric interpretation of integrals, making abstract mathematical concepts more accessible to learners at various levels. This visual-analytical hybrid approach has proven particularly effective in educational settings where students struggle with conventional integration techniques.
Furthermore, intégrammes have found applications in fields ranging from physics and engineering to economics and data analysis. Their ability to represent complex mathematical relationships in an intuitive format makes them invaluable for professionals who need to communicate mathematical concepts to non-mathematical audiences.
Basic Principles and Formulas Behind Intégrammes
The foundation of intégrammes rests on several key mathematical principles that distinguish them from standard integration approaches. At their core, intégrammes utilize a combination of visual mapping and algebraic transformation to solve integration problems.
Core Formula Structure
The basic intégramme formula follows this pattern:
∫[a,b] f(x)dx = Σ[visual components] + analytical correction terms
This formula represents the integration of function f(x) over the interval [a,b], where the visual components correspond to geometric interpretations of the area under the curve, and the analytical correction terms account for any discrepancies between the visual approximation and the exact solution.
Visual Representation Elements
Intégrammes incorporate three primary visual elements:
Grid overlays that help estimate areas under curves through geometric approximation. These grids can be adjusted for different levels of precision, allowing users to balance computational efficiency with accuracy requirements.
Color-coded regions that represent different aspects of the integration process, such as positive and negative areas, or regions requiring different integration techniques.
Interactive scaling that enables users to zoom in on specific portions of the integration domain, facilitating detailed analysis of complex functions.
Mathematical Properties
Intégrammes maintain all the fundamental properties of traditional integrals, including linearity, additivity over intervals, and the fundamental theorem of calculus. However, they extend these properties through their visual framework, providing additional insights into the behavior of integrated functions.
Step-by-Step Guide to Solving Intégrammes
Mastering intégrammes requires a systematic approach that combines visual analysis with mathematical rigor. Here’s a comprehensive method for tackling intégramme problems effectively.
Step 1: Function Analysis and Setup
Begin by carefully examining the function you need to integrate. Plot the function over the specified interval, paying particular attention to:
- Discontinuities or undefined regions
- Areas where the function crosses the x-axis
- Regions of rapid change or unusual behavior
- Boundary conditions at the integration limits
Create your initial intégramme framework by establishing a coordinate system that clearly displays these key features.
Step 2: Visual Approximation
Apply the grid overlay technique to estimate the integral visually. Start with a coarse grid to get a rough approximation, then progressively refine the grid resolution in areas where greater precision is needed.
Use the color-coding system to distinguish between positive and negative contributions to the integral. This visual separation helps prevent sign errors that commonly occur in traditional integration methods.
Step 3: Analytical Verification
Once you have a visual estimate, apply traditional integration techniques to verify and refine your result. The visual approximation serves as a valuable check against computational errors and provides intuitive confirmation of your analytical work.
Calculate the analytical correction terms by comparing your visual estimate with the exact analytical result. These correction terms often reveal important properties of the function that might not be immediately apparent through purely algebraic approaches.
Step 4: Result Integration and Interpretation
Combine your visual and analytical results to produce the final intégramme solution. Document both the numerical result and the insights gained through the visual analysis process.
Advanced Techniques and Applications
As you become more comfortable with basic intégramme methods, several advanced techniques can significantly expand your problem-solving capabilities.
Multi-dimensional Intégrammes
Advanced practitioners often work with intégrammes involving functions of multiple variables. These problems require sophisticated visualization techniques, including:
Contour mapping for functions of two variables, where level curves help identify regions of integration and potential computational challenges.
Cross-sectional analysis for three-dimensional problems, breaking complex volume integrals into manageable two-dimensional components.
Parametric representation for integrals involving curves and surfaces that don’t align naturally with standard coordinate systems.
Specialized Applications
Intégrammes have proven particularly valuable in several specialized areas:
Engineering applications often involve intégrammes when calculating moment of inertia, center of mass, or fluid flow properties. The visual component helps engineers understand the physical significance of their calculations.
Economic modeling uses intégrammes to represent consumer surplus, producer surplus, and other economic quantities where the visual representation aids in policy interpretation and communication.
Physics applications include electromagnetic field calculations, quantum mechanical probability distributions, and thermodynamic property evaluations.
Computational Integration
Modern intégramme techniques often incorporate computational tools that automate the visual approximation process while maintaining the interpretive benefits of the visual approach. These tools can handle functions that would be difficult or impossible to visualize manually while preserving the intuitive understanding that makes intégrammes valuable.
Tips and Tricks for Mastering Intégrammes
Developing expertise in intégrammes requires practice and attention to several key strategies that can significantly improve your efficiency and accuracy.
Optimization Strategies
Start with simple cases before attempting complex problems. Build your intuition with functions you can easily visualize and verify analytically.
Develop a consistent workflow that you can apply systematically to different types of problems. This consistency reduces errors and builds confidence in your results.
Maintain detailed documentation of your visual approximations and analytical calculations. This documentation proves invaluable when reviewing your work or explaining your methods to others.
Common Pitfalls and Solutions
Many students encounter predictable challenges when learning intégrammes. Scale sensitivity represents one of the most common issues—choosing an inappropriate scale for your visual representation can lead to significant errors in your approximation.
Sign management requires careful attention, particularly when dealing with functions that change sign over the integration interval. The color-coding system helps, but systematic checking remains essential.
Precision balance involves finding the right level of detail for your visual approximation. Too little detail produces inaccurate results, while excessive detail can make the problem unnecessarily complex.
Building Mathematical Intuition
Regular practice with intégrammes develops mathematical intuition that extends far beyond integration problems. The visual-analytical connection strengthens your understanding of mathematical relationships and improves your ability to estimate and verify results in other areas of mathematics.
Expanding Your Mathematical Toolkit
Understanding intégrammes opens doors to a more intuitive and comprehensive approach to mathematical problem-solving. The combination of visual insight and analytical rigor that defines intégrammes represents a valuable addition to any mathematician’s toolkit.
The techniques and principles covered in this guide provide a solid foundation for exploring more advanced applications and developing your own innovative approaches to mathematical challenges. As you continue practicing with intégrammes, you’ll likely discover new connections between visual representation and analytical techniques that enhance your overall mathematical understanding.
Consider starting with simple polynomial functions to build your confidence, then gradually progressing to more complex functions as your skills develop. The investment in mastering intégrammes pays dividends not only in integration problems but in developing a deeper appreciation for the geometric beauty underlying mathematical analysis.